Preconditioned Nonlinear Conjugate Gradient Method for Real-time Interior-point Hyperelasticity

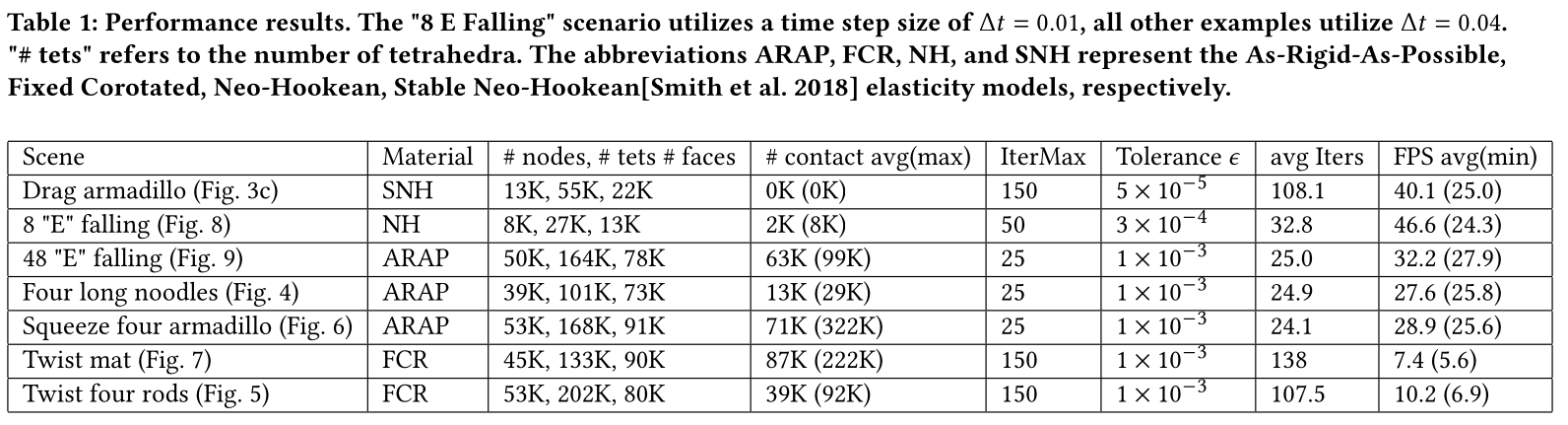
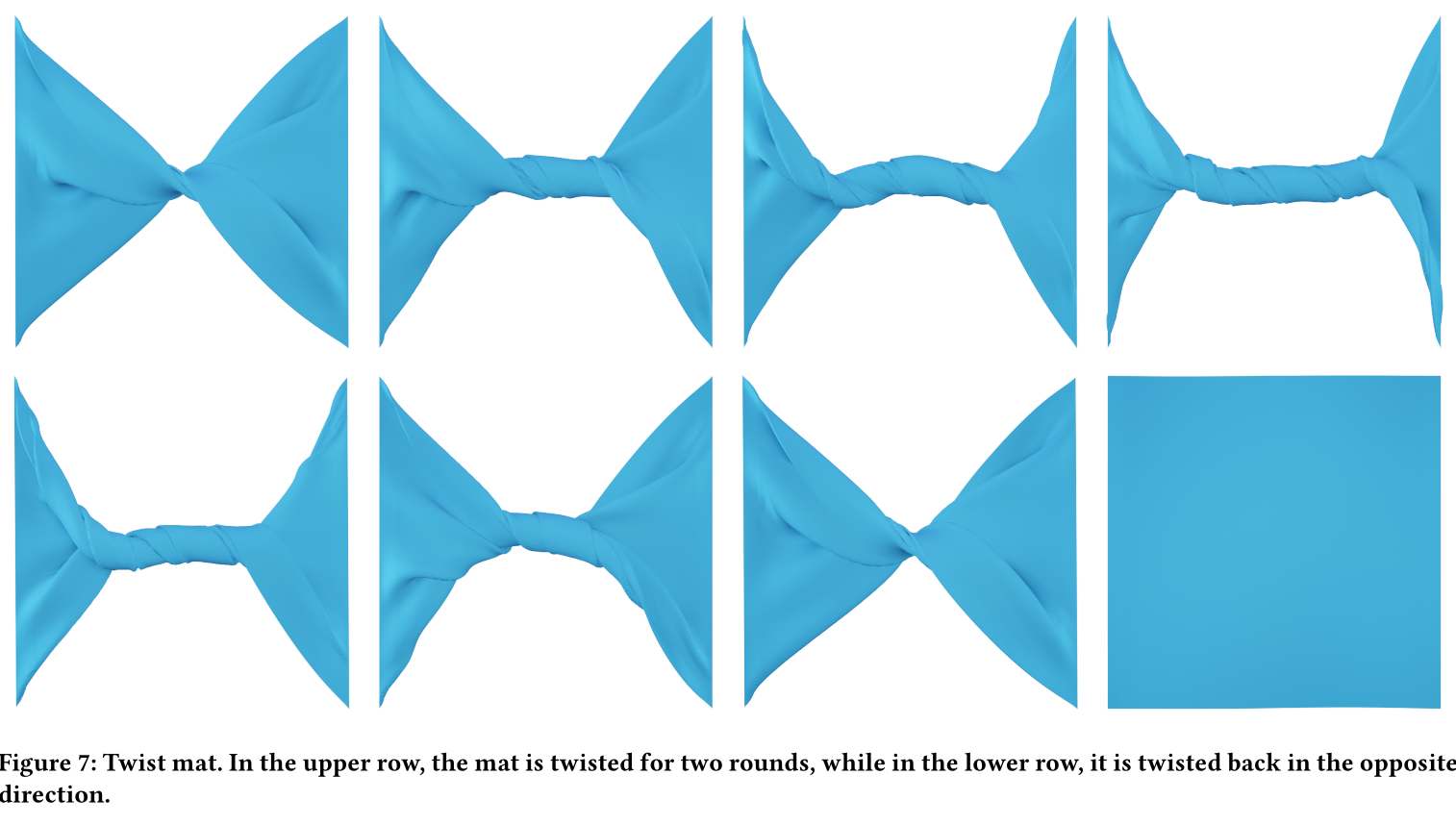
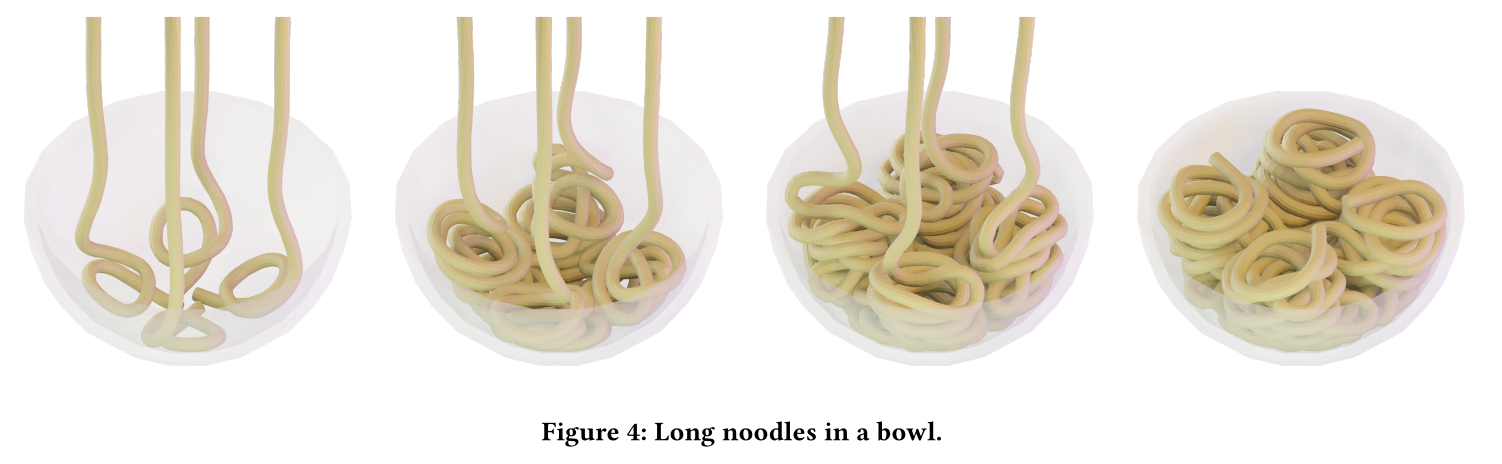
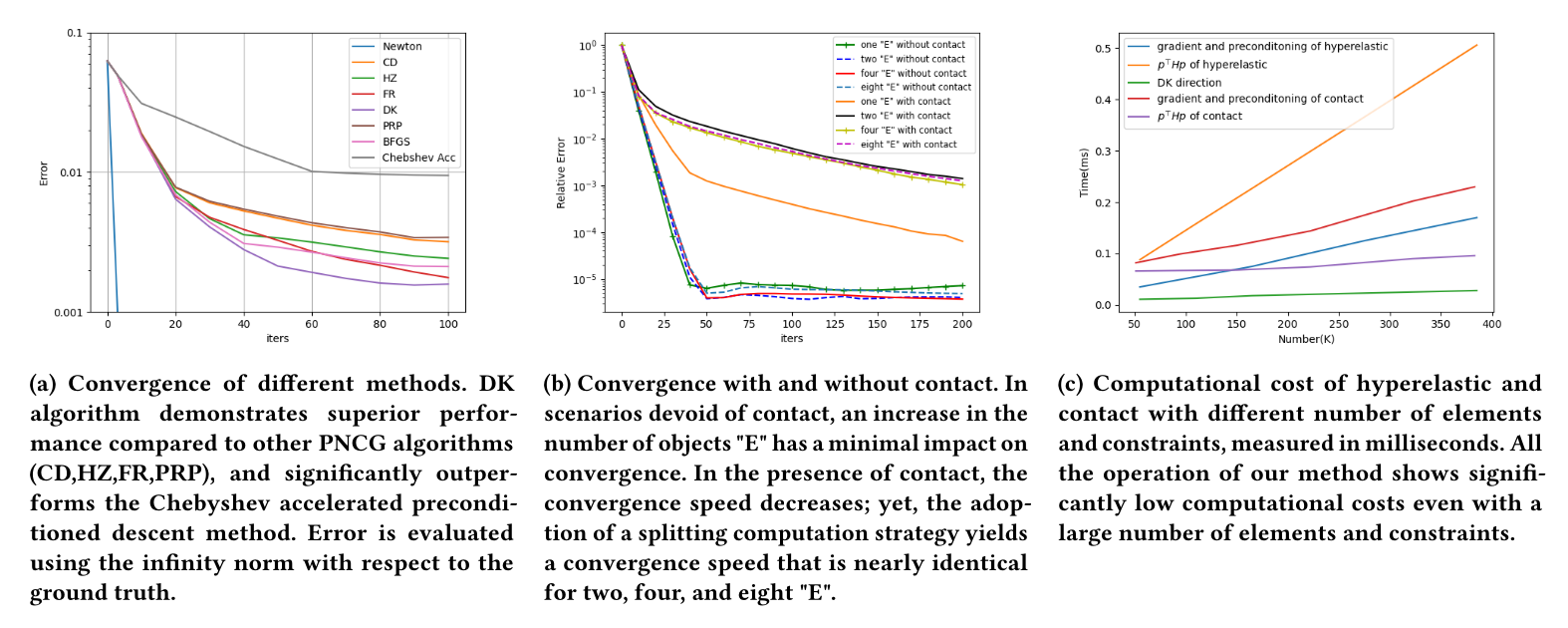
The linear conjugate gradient method is widely used in physical simulation, particularly for solving large-scale linear systems derived from Newton’s method. The nonlinear conjugate gradient method generalizes the conjugate gradient method to nonlinear optimization, which is extensively utilized in solving practical large-scale unconstrained optimization problems. However, it is rarely discussed in physical simulation due to the requirement of multiple vector-vector dot products. Fortunately, with the advancement of GPU-parallel acceleration techniques, it is no longer a bottleneck. In this paper, we propose a Jacobi preconditioned nonlinear conjugate gradient method for elastic deformation using interior-point methods. Our method is straightforward, GPU-parallelizable, and exhibits fast convergence and robustness against large time steps. The employment of the barrier function in interior-point methods necessitates continuous collision detection per iteration to obtain a penetration-free step size, which is computationally expensive and challenging to parallelize on GPUs. To address this issue, we introduce a line search strategy that deduces an appropriate step size in a single pass, eliminating the need for additional collision detection. Furthermore, we simplify and accelerate the computations of Jacobi preconditioning and Hessian-vector product for hyperelasticity and barrier function. Our method can accurately simulate objects comprising over 100,000 tetrahedra in complex self-collision scenarios at real-time speeds.